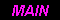兩/4挿摨幉働乕僽儖偵傛傞嫟怳僩儔僢僾
丂嫟怳偵偼丒丒丒
嘆廤拞掕悢(LC)嫟怳丒丒丒偄傢備傞僐僀儖偲僐儞僨儞僒偵傛傞冎L亖1/冎C偺悽奅
嘇慄楬嫟怳丒丒丒宱楬挿傗摨幉挿偵傛傞嫟怳(HF傾儞僾偱傕V/UHF懷偺慄楬嫟怳偑偁傞)
嘊嬻摯嫟怳丒丒丒嬻摯撪偱婲偙傞嫟怳(庡偵儅僀僋儘僂僃乕僽)
丒丒丒偑偁傞偑峏偵丒丒丒
嘋忋婰偑棈傒崌偆嫟怳丒丒丒幚憰偡傞偲偙偺忬懺偵帄傞応崌偑懡偄
丒丒丒偑偁傞帠傪崅廃攇傪庢傝埖偆応崌偼怱摼偰偍偔昁梫偑偁傞丅
丂嫟怳廃攇悢偼丄偦傟偧傟傪暘晍掕悢夞楬偲偟偰峫嶡偡傟偽崕柧偵夝愅偱偒傞丅偟偐偟HF埲壓偺斾妑揑掅偄廃攇悢偱偼丄扨弮偵L偲C偺廤拞掕悢夞楬偲偟偰懆偊偰偟傑偆応崌偑杦偳偱偁傠偆丅幚偼偙傟偩偗偱偼曅庤棊偪側偺偱偁傞丅
丂V/UHF懷堟偵側傞偲栚揑廃攇悢偱嫟怳偑摼傜傟側偐偭偨傝丄巚偄傕傛傜偸廃攇悢偱嫟怳偟偨傝偡傞丅椺偊偽VC傪擖傟(惷揹梕検憹壔)嫟怳廃攇悢傪壓偘傛偆偲偟偰傕壓偑傜偢丄媡偵忋偑偭偨傝偡傞偙偲傕100MHz埲忋偺悽奅偱偼椙偔懱尡偡傞丅傑偨儕僯傾傾儞僾偱偼丄栚揑埲奜偺偲傫偱傕側偄廃攇悢偱婑惗敪怳偟偨傝帺屓敪怳偡傞応崌偑偁傞丅
丂偙傟傜偼廤拞掕悢夞楬偲偟偰尒偰偄傞尷傝尨場偺媶柧偼墦偄偩傠偆丅夞楬恾偩偗偱偼幚憰帪偺宱楬挿傪攃埇偡傞帠偼旕忢偵擄偟偄丅廤拞掕悢埲奜偺嫟怳偺壜擻惈偵偮偄偰丄傑偨暘晍掕悢揑側帇揰偑側偄偲夝寛偵帄傜側偄壽戣偲尵偊傞丅
丂幚偼丄杦偳偺幚憰夞楬偱慜弍偺嘆偲嘇偑摨帪偵懚嵼偟偰偄傞丅廤拞掕悢嫟怳偺姶妎偵慄楬嫟怳傪壛枴偟偨姶妎傪帩偪懕偗傞帠偑戝愗偱偁傞丅偙偺姶妎偑偁傟偽慜弎偺晄壜夝側尰徾偵偮偄偰棟夝偺巺岥偵偮側偑傞偼偢偱偁傞丅
丂丒丒丒梋択偩偑丄VHF-PA偱恀嬻娗偺弌椡惷揹梕検偺懡偝偵庤傪從偄偰偄傞応崌偼丄愊嬌揑偵慄楬嫟怳傪庢傝擖傟栚揑傪壥偨偡帠偑弌棃傞丅
丂偝偰島庍偑挿偔側偭偨偑丄偙偙偱偼乽兩/4摨幉働乕僽儖乿偺帩偮嫟怳摿惈傪棙梡偟偰崅挷攇僩儔僢僾傪嶌偭偰傒偨丅戝嶨攃側僀儊乕僕偲偟偰丄兩/4慄楬偼愭抂傪抁棈偡傞偲Z亖亣丄奐曻側傜Z亖0偺抣傪偲傞丅廃攇悢偑攞偵側傞偲偦偺忬嫷偼斀揮偟偰偄偔偺偱丄椺偊偽145MHz偱Z亖亣偺慄楬偼丄攞偺290MHz偱偼Z亖0偲側傞丅偙偺尰徾偼攞丒攞偱孞傝曉偝傟傞偺偱丄嬼悢攞偲婏悢攞偱埲壓偺擛偔曄壔偡傞丅
丂丂丂丂丂1攞亖145MHz丒丒丒亣丂丂丂丂5攞亖725MHz丒丒丒亣丂丂丂丂9攞亖1305MHz丒丒丒亣
丂丂丂丂丂2攞亖290MHz丒丒丒0丂丂丂丂丂6攞亖870MHz丒丒丒0丂丂丂丂丂丂丂丂丂丂丒
丂丂丂丂丂3攞亖435MHz丒丒丒亣丂丂丂丂7攞亖1015MHz丒丒丒亣丂丂丂丂丂丂丂丂丂丒
丂丂丂丂丂4攞亖580MHz丒丒丒0丂丂丂丂丂8攞亖1160MHz丒丒丒0丂丂丂丂丂丂丂丂 丂丒
丂偙偺応崌0偵側傞廃攇悢偱僩儔僢僾岠壥傪摼傞帠偑弌棃傞丅側偍愭抂奐曻偺摨幉働乕僽儖偺応崌偼亣偲0偑斀揮偡傞丅扐偟愭抂奐曻偱偼崅廃攇偺楻傟偑偁傞偨傔愭抂抁棈偱巊梡偡傞応崌偑杦偳偱偁傞丅
丂側偍摨幉働乕僽儖偼桿揹懱傪巊梡偡傞偺偱懍搙學悢偑偁傞丅幚挿偼嶼弌偟偨兩/4挿偵學悢乮億儕僄僠儗儞摨幉側傜0.67乯傪妡偗偨挿偝偵側傞丅
 丂椺偊偽145MHz側傜l亖乮兩/4乯丒0.67亖(300/145x4)丒0.67亖0.346m丅幨恀偼8D-2W偱惢嶌偟偨144MHz僶儞僪偵巊梡偡傞2攞偺崅挷攇僩儔僢僾偲偦偺摿惈帋尡拞偺僗僫僢僾丅
丂椺偊偽145MHz側傜l亖乮兩/4乯丒0.67亖(300/145x4)丒0.67亖0.346m丅幨恀偼8D-2W偱惢嶌偟偨144MHz僶儞僪偵巊梡偡傞2攞偺崅挷攇僩儔僢僾偲偦偺摿惈帋尡拞偺僗僫僢僾丅
丂NJ-NPx2偺T宆暘婒偵丄NP僐僱僋僞偱惢嶌偟偨僩儔僢僾傪庢傝晅偗偰偄傞丅僩儔僢僾偺愭抂偼丄摨幉栐慄傪夝偟墌廃忋偐傜恈慄偵廤拞偝偣僴儞僟傪棳偡丅偙偺偲偒RF偑楻傟側偄傛偆偵怲廳偵峴側偆丅
丂偙傟偩偗偱傕PA扨懱偱彍嫀偱偒側偐偭偨崅挷攇偺梷埑偵岠壥偑偁傞丅梷埑偝傟偨崅挷攇偼儕僞乕儞夞楬偵棳傟崬傓偺偱僐儌儞儌乕僪鐃幩偼偙偺尷傝偱偼側偄偺偱拲堄丅
嶲峫嘆丗擟堄挿l(m)偺愭抂僔儑乕僩慄楬偺Zs丒丒丒
丂丂丂丂丂Zs = jZc丒tan兝l丂乮Zc丗慄楬摿惈僀儞僺乕僟儞僗丄l丗慄楬挿丄兝丗2兾/兩乯
丂丂丂丂丂丂 = jZc丒tan(2兾/兩)丒(兩/2)丒丒丒l=(兩/2)偼2攞廃攇悢偱偺挿偝
丂丂丂丂丂丂 = jZc丒tan兾
丂丂丂丂丂丂 = jZc丒0
丂丂丂丂丂丂 = 0(兌)
嶲峫嘇丗兩/4慄楬偺擖椡懁偐傜愭抂(抁棈)傑偱偺僀儞僺乕僟儞僗偼亣佁0傪偲傞偺偱丄暲楍嫟怳摿惈傪帩偭偨僀儞僺乕僟儞僗曄姺(僩儔
丂丂丂丂丂儞僗)偲偟偰傕妶梡偱偒傞丅側偍兩/2慄楬偱偼0佁亣佁0傪偲傝捈楍嫟怳偲偟偰棙梡偱偒傞丅
丂丂丂丂丂傑偨愭抂奐曻偺応崌偼偙傟傜偺媡偺抣傪偲傞丅
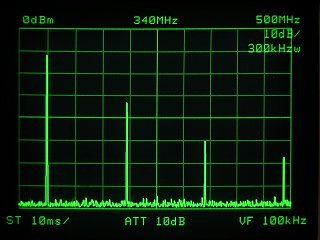
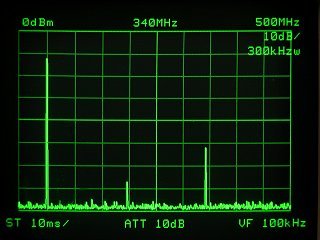
丂忋偼145MHz(CW)傪曻傝崬傫偩帪偺僗儁傾僫幨恀偱丄嵍偑SG弌椡丄塃偑僩儔僢僾傪庢傝晅偗偨忬懺偺傕偺丅僩儔僢僾偺岠壥偵傛傝丄2師崅挷攇(290MHz)偱栺-34dB丄4師崅挷攇(580MHz)偱偼僲僀僘儗儀儖傑偱尭悐偟偰偄傞丅扐偟3師崅挷攇(435MHz)偵偮偄偰偼棟榑捠傝岠壥偑柍偄偙偲偑暘傞丅
丂側偍慜弎偺擛偔丄偁偔傑偱僲乕儅儖儌乕僪偱偺忬嫷側偺偱丄梷埑偝傟偰儕僞乕儞夞楬傪栠傞怣崋偵偮偄偰偼鉃懱鐃幩偺梫場偲側傝丄僐儌儞儌乕僪僲僀僘偲偟偰鐃幩偝傟傞壜擻惈偑偁傞丅偙偺応崌偼僩儔僢僾捈屻偵僐儌儞儌乕僪僼傿儖僞乕偺憓擖偑昁梫偵側傞丅