Fractal: Dragon Curve (WPF
with C#)
|
Applied rule of recursive
drawing
 |
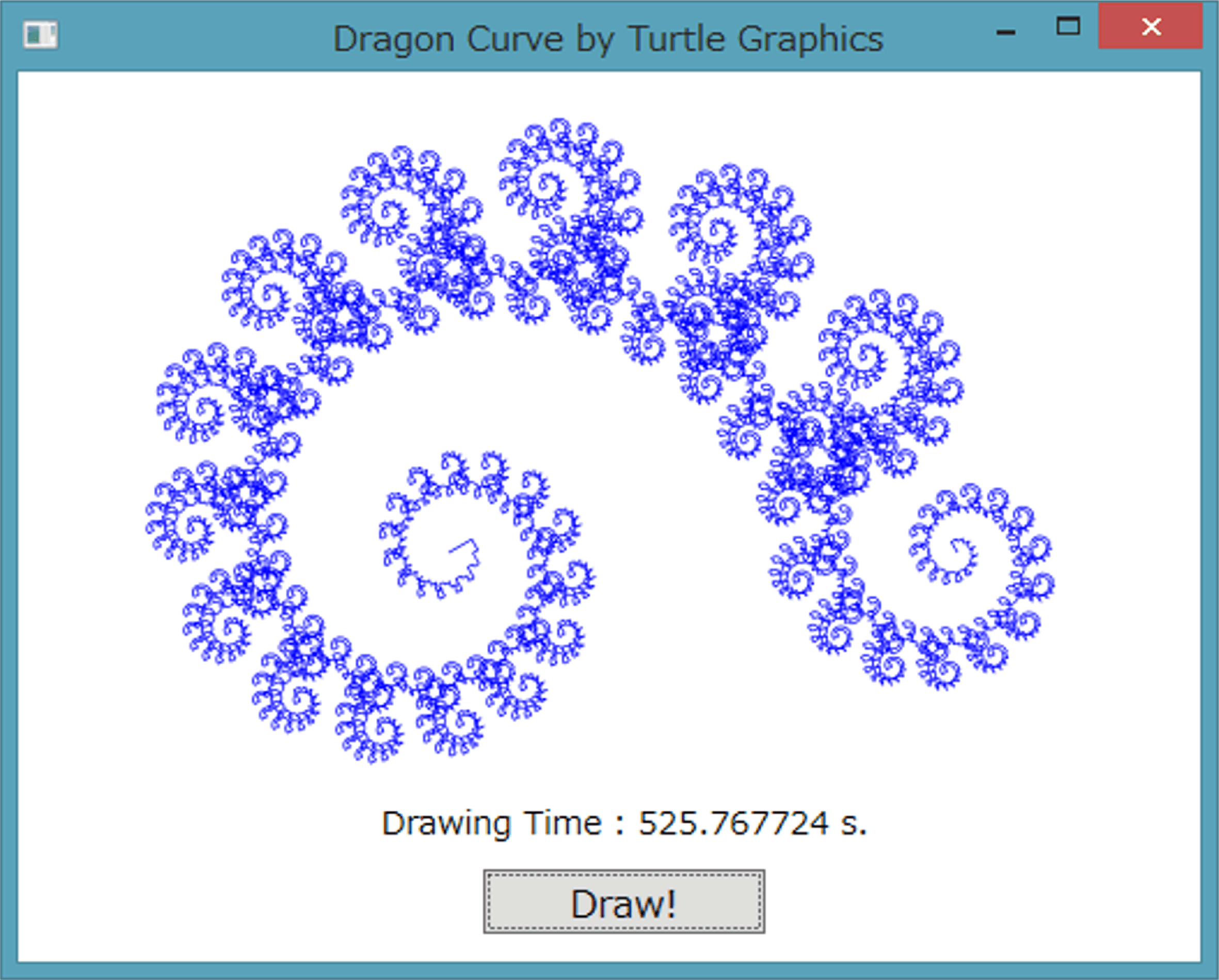 It seems that some of the unmovable points (the green points shown in the left figure) are located at a specific position in each periodic pattern in the drawn curve. |
| This
figure indicates an applied rule of recursive drawing. When
the complexity order is increased, additional green points and
new red-lined paths are generated in the same manner. Here, two sets of fractional ratios of {cos 25o and sin 25o} or {sin 25o and cos 25o} in length and turning angles of {25o in
left, 90o in right and 65o in
left} or {65o in right, 90o in left and 25o
in right} are alternately inherited
for all the order. |
| //
DragonCurve_Turtle_WPF_001\MainWindow.xaml.cs // Dragon Curve // (WPF application with C# // on Microsoft Visual Studio Express 2013 for Windows Desktop) // Oct. 29, 2014, by Masao Sakuraba // (Ref. 1-5 guided me to this program.) // * NOTE1: Blue-color parts were automatically generated by Visual Studio. // * NOTE2: Red-color parts were newly added. using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; using System.Windows; using System.Windows.Controls; using System.Windows.Data; using System.Windows.Documents; using System.Windows.Input; using System.Windows.Media; using System.Windows.Media.Imaging; using System.Windows.Navigation; using System.Windows.Shapes; using System.Diagnostics; // Namespace for class "Stopwatch". using ThinkLib; // After adding the file "ThinkLib.dll" as a reference [2]. namespace DragonCurve_Turtle_WPF_001 { /// <summary> /// MainWindow.xaml の相互作用ロジック /// </summary> public partial class MainWindow : Window { Turtle pen1; // Make a turtle using ThinkLib [3]. double PI = 3.141592654; void PatternGenerator1(Turtle _pen, double _length, int _complexity) { if (_complexity == 0 | _length < 2.4) { _pen.Forward(_length); } else { _pen.Left(25); PatternGenerator1(_pen, _length * Math.Cos(PI / 180 * 25), _complexity - 1); _pen.Right(90); // Cross recursion [4]. PatternGenerator2(_pen, _length * Math.Sin(PI / 180 * 25), _complexity - 1); _pen.Left(65); } } void PatternGenerator2(Turtle _pen, double _length, int _complexity) { if (_complexity == 0 | _length < 2.4) { _pen.Forward(_length); } else { _pen.Right(65); PatternGenerator1(_pen, _length * Math.Sin(PI / 180 * 25), _complexity - 1); _pen.Left(90); PatternGenerator2(_pen, _length * Math.Cos(PI / 180 * 25), _complexity - 1); _pen.Right(25); } } public MainWindow() { InitializeComponent(); pen1 = new Turtle(playground); // After making Canvas in MainWindow // with the Canvas name of "playground" [3]. pen1.Visible = false; // When you do not like showning a turtle [5]. } private void Button1_Click(object sender, RoutedEventArgs e) { // After making Button for Event Handler. double Length = 220.0; int Complexity = 30; pen1.Clear(); pen1.LineBrush = Brushes.Blue; pen1.BrushWidth = 0.7; pen1.WarpTo(Length * 0.8, Length * 0.9); Stopwatch TimeMeasure = new Stopwatch(); // Make a stopwatch. TimeMeasure.Start(); PatternGenerator1(pen1, Length, Complexity); double Time_in_s = (TimeMeasure.Elapsed).TotalSeconds; Label1.Content = ("Drawing Time : " + Time_in_s + " s."); } } } |
Reference
(1)
"Think Sharply with C#" by Prof. Peter Wentworth (Rhodes Univ.),
http://www.ict.ru.ac.za/resources/ThinkSharply/thinksharply/
(2) "Appendices :
Getting Started with ThinkLib",
http://www.ict.ru.ac.za/Resources/ThinkSharply/ThinkSharply/thinklib_getting_started.html
(3) "Chapter 7
: Hello, little turtles!",
http://www.ict.ru.ac.za/Resources/ThinkSharply/ThinkSharply/hello_little_turtles.html
(4) "Chapter
21 : Recursion",
http://www.ict.ru.ac.za/Resources/ThinkSharply/ThinkSharply/recursion.html
(5)
"Appendices : ThinkLib.Turtle Documentation",
http://www.ict.ru.ac.za/Resources/ThinkSharply/ThinkSharply/thinklib_turtle_docs.html
This home page is produced by KompoZer (free and open software).