
|
お釣りの暗算
|
|
| 掲載日 | 2009年5月31日 |
| 情報提供者 | AKILA |
|
956円の買物の時に1006円の預かり金を受け取るなど、お釣りの端数をキレイにそろえるため、預かり金自体に端数がある場合があります。 もちろんレジに預かり金を打ち込んで精算すれば「お釣り 50円」と計算してくれますが、これをレジに頼らず暗算できるようになると何かと便利です。 預かり金をレジに打ち間違ったときや、お客様が間違った預かり金(あまり意味のない端数)を出してきたとき (5506円の買物で10015円の預かり金の時 → お釣りは4509円)など、レジで計算しなくても正しいお釣りが分かると戸惑うことが無くなります。 一番役に立つのは自分が客側に立ったときですが…。 この暗算法には2通りのやり方があります。 ひとつはお釣りに端数を加算する加算法(と勝手に命名)、 もうひとつは端数を預かり金から最初に減算しておく減算法(と勝手に命名)です。 やり方は下記の通り。 ■■■■■■■■ 加算法 ■■■■■■■■ まずは加算法です。 例: 商品代金額 2618円 預かり金額 3118円 まず最初に預かり金額の端数をいったん忘れます。 例で言うと3118円の端数118円を無かったことにします。 そうすると預かり金額は3000円ですね。 この預かり金額でお釣りを計算します。 3000円 − 2618円 = 382円 こうやって計算したお釣りの382円に、先ほど無かったことにした端数118円を加算します。 382円 + 118円 = 500円 これが最終的なお釣りです。 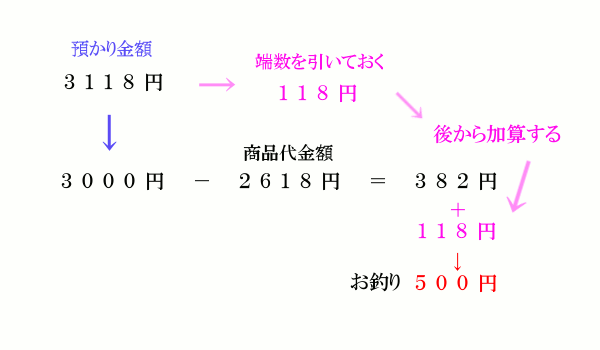
え? そもそも 3000円 − 2618円 = 382円 がすぐに浮かばない? これにもコツがあります。 最上位桁は [ 預かり金の数字 (例では3) ] − [ 商品代金の数字 (例では2) ] − 1 → 0 最下位桁は 10 − [ 商品代金の数字 (例では8) ] → 2 それ以外の中間桁は 9 − [ 商品代金の数字 (例では6と1) ] → 3 と 8 で計算すると憶えてください。 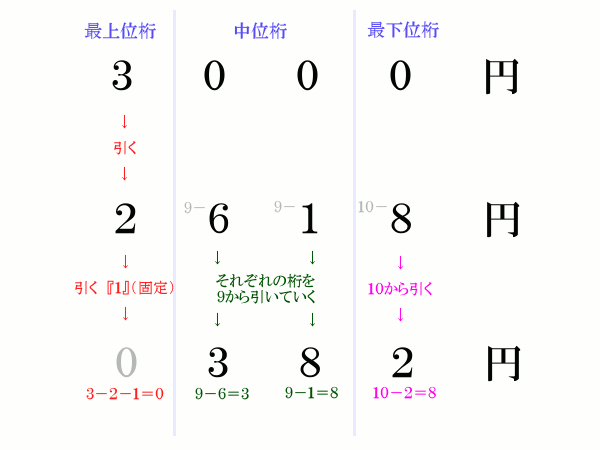 ■■■■■■■■ 減算法 ■■■■■■■■ つぎに減算法です。 例: 商品代金額 2618円 預かり金額 3118円 まず最初に預かり金の端数を切り捨てるのですが、その際に同じ金額を商品代金からも切り捨てます。 例で言うと3118円の端数118円を切り捨てて3000円にするのと同時に、商品代金の2618円からも118円を切り捨てます(減算する)。 2618円 − 118円 = 2500円 あとはそれぞれの金額を使ってお釣りを計算します。 3000円 − 2500円 = 500円 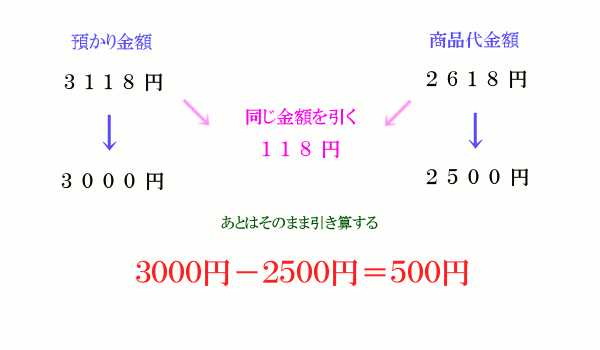
どうでしょうか? やり方は分かりましたか? 加算法と減算法のどちらが優れているとかオススメとか言うわけではありません。 使いやすい方を使えばいいですし、両方を使い分けても良いでしょう。 私の場合はどちらかと言えば減算法をよく使い、減算法を使っても瞬時に答えが思い浮かばない場合は加算法に切り替えて計算しています。 |
|
|
|
|
|
□ □ 広 告 □ □ |