使用キャラは陸遜
ステージは無双モードの合肥新城包囲戦
クリアタイム約9分半
コンボポイント965
試行回数1096回
| ラベル | 名称 | 出現回数 | 新限界値達成数 | 出現総数に対する 出現率 |
出現総数に対する 新限界値達成率 |
出現数に対する 新限界値達成率 |
| 1 | 神速符 | 39 | 7 | 0.035584 | 0.006387 | 0.179487 |
| 2 | 翔靴 | 71 | 20 | 0.064781 | 0.018248 | 0.28169 |
| 3 | 青龍胆 | 41 | 3 | 0.037409 | 0.002737 | 0.073171 |
| 4 | 朱雀翼 | 76 | 3 | 0.069343 | 0.002737 | 0.039474 |
| 5 | 白虎牙 | 73 | 8 | 0.066606 | 0.007299 | 0.109589 |
| 6 | 玄武甲 | 68 | 8 | 0.062044 | 0.007299 | 0.117647 |
| 7 | 黄忠弓 | 63 | 7 | 0.057482 | 0.006387 | 0.111111 |
| 8 | 藤甲鎧 | 60 | 10 | 0.054745 | 0.009124 | 0.166667 |
| 9 | 羌族角 | 61 | 5 | 0.055657 | 0.004562 | 0.081967 |
| 10 | 騎甲鎧 | 68 | 8 | 0.062044 | 0.007299 | 0.117647 |
| 11 | 七星玉 | 59 | 9 | 0.053832 | 0.008212 | 0.152542 |
| 12 | 真空書 | 10 | 3 | 0.009124 | 0.002737 | 0.3 |
| 13 | 活丹 | 4 | 0 | 0.00365 | 0 | 0 |
| 14 | 弓仙箙 | 54 | 8 | 0.04927 | 0.007299 | 0.148148 |
| 15 | 仙丹袋 | 63 | 10 | 0.057482 | 0.009124 | 0.15873 |
| 16 | 溜力膏 | 64 | 16 | 0.058394 | 0.014599 | 0.25 |
| 17 | 護衛朱雀翼 | 26 | 2 | 0.023723 | 0.001825 | 0.076923 |
| 18 | 護衛青龍胆 | 23 | 4 | 0.020985 | 0.00365 | 0.173913 |
| 19 | 護衛白虎牙 | 30 | 5 | 0.027372 | 0.004562 | 0.166667 |
| 20 | 護衛玄武甲 | 34 | 8 | 0.031022 | 0.007299 | 0.235294 |
| 21 | 護衛黄忠弓 | 27 | 5 | 0.024635 | 0.004562 | 0.185185 |
| 22 | 護衛藤甲鎧 | 21 | 6 | 0.019161 | 0.005474 | 0.285714 |
| 23 | 護衛神速符 | 25 | 9 | 0.02281 | 0.008212 | 0.36 |
| 24 | 護衛真空書 | 2 | 1 | 0.001825 | 0.000912 | 0.5 |
| 25 | 護衛活丹 | 34 | 9 | 0.031022 | 0.008212 | 0.264706 |
よって総出現数に対する護衛兵アイテムの出現率は222/1096≒0.2025≒1/5となる。
かなり綺麗な数字にまとまったところをみると、ほぼ1/5で確定であると推察される。
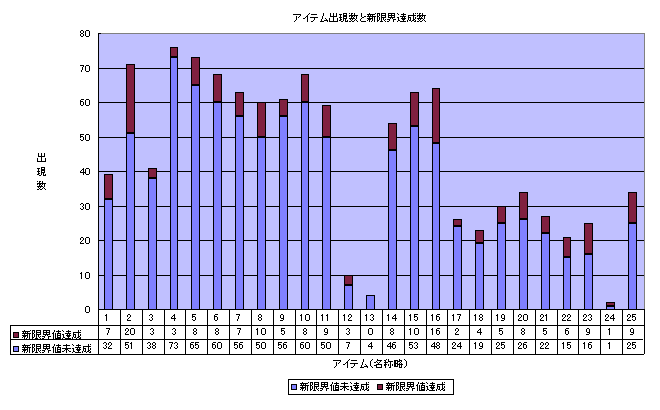
ラベル1〜16の通常アイテムの範囲内で特に目立つのは12と13の出現数の少なさと、次いで少ない1と3の出現数である。
そこで(2、4〜11、14〜16)の平均から推測される確率を求めてみると、約15/255となる。
では1、3の出現数は15/255の誤差の範囲内であるのかどうかを検定してみる。
詳しい方法は省略するが(どうしても知りたければ確率統計学の書籍を読んでくれ)、95%の確率で15/255ではないと分かる。
次に、1〜16の範囲で最も出現数の少ない13の出現率を計算すると0.00445≒1/255となる。
上でさも当たり前のように確率の分母に255を用いたのはこのため。
プログラム的にも255という数字はキリがいいので、おそらく分母は255で間違いないだろう。
ではこの出現率を元に1〜16のアイテムの出現率を求めると次のようになる。
1,3=12/255(±4/255)
2、4〜11、14〜16=19/255(±2/255)
12=2/255(+17/255〜−1/255)
13=1/255(+11/255)
*括弧内は測定誤差の範囲
では次に17〜25のアイテムの出現率を考えてみる。
まず明かに出現率の少ない24の出現率を求めてみると、2/255となる。
次に残りのアイテムの出現率を同じものと過程して確率を求めると、およそ31.5/255となる。
しかし、分子に少数が現れるということは考えにくいため「残りのアイテムの出現率は全て同じ」という仮定が間違っていることになる。
だがサンプル数が少ないため、このデータからではどうしても測定誤差が±4.3%出てしまう(≒±11/255)。
では測定誤差を抑えるためにはどの程度のサンプルが必要なのか。
仮に測定誤差を±2%に抑えると仮定して必要サンプル数を求めると、およそ1039個と分かる。
現在既にあるサンプル数222個を差し引いたおよそ800個を入手するためには時間にしておよそ66.6時間必要となる。
いくらなんでもそんなに集めることは不可能に近いため、仕方がないので以下に「17〜23、25の出現率が同じ」という仮定を前提とした出現率を表記する。
17〜23、25=31.5/255(±11/255)
24=2/255(+3/255〜−1/255)
*括弧内は測定誤差の範囲