いきなり始まった新シリーズ、学術系小ネタの第一回です。
今回は「地球上の任意の２点間の緯度・経度がわかっている時のこれらの最短経路距離について」の話題です。
地球の表面は、当たり前ですが球面状です。正確には西洋梨のように少しいびつな形をしていますが、誤差の範囲とします。
球面のような曲面では、任意の２点間における最短経路距離を求めるのにちょっとめんどくさいことをしなければなりません。球面上における任意の２点間の距離は、座標平面上で距離を求めた様な方法を用いるのではなく、球の中心からそれぞれの点に引いた２直線の傾きから、距離を算出する必要があります。
どのように計算するのかを以下に示します。
地球上に与えられている座標系として緯度と経度がありますが、これはグリニッジ天文台を経度ゼロ度、赤道を緯度ゼロ度とした地球の中心から見た傾きの度合いを表した数値であることに注意してください。座標空間上に与えられた球面の上にある点の位置は、球の中心からどの方向にあるかさえわかれば一意的に決まる、ということからこのような決まりとなっています（ほんとは少し違うけど）。
いいかげん計算に入りましょう。
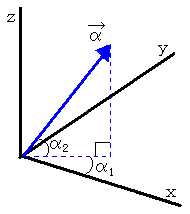
上の図にあるベクトルαは、原点を中心とした半径ｒの球面上にあるものとします。このベクトルの長さはｒ、ベクトルαをｘｙ平面に垂直に降ろした直線と、ｘ軸とのなす角をα１、ベクトルαとｘｙ平面とのなす角をα２とします（ｒ、α１、α２はそれぞれ地球の半径、経度、緯度に相当します。ちなみにこの図だと、東＆北が正の方向、西＆南が負の方向となります）。このときベクトルαの終点の座標をｒ、α１、α２で表すと次のようになります。
α＝（ｒcosα２cosα１，ｒcosα２sinα１，ｒsinα２）
本題は「球面上にある任意の２点間の経路距離（球面上での最短距離）」を求めることなので、もう１つのベクトルβを同じように定義します。
β＝（ｒcosβ２cosβ１，ｒcosβ２sinβ１，ｒsinβ２）
で、このαとβのなす角を求めます。これは、三角関数の公式
cosθ＝[αβ]／｜α｜｜β｜
※ここで、[αβ]はαとβの内積を、｜α｜と｜β｜はそれぞれαとβの長さを表します。
を用いれば良いので、これを適用すると、
cosθ＝（ｒcosα２cosα１×ｒcosβ２cosβ１＋ｒcosα２sinα１×ｒcosβ２sinβ１＋ｒsinα２×ｒsinβ２）／（ｒ×ｒ）
＝cosα２cosα１cosβ２cosβ１＋cosα２sinα１cosβ２sinβ１＋sinα２sinβ２
で、この値から、なす角θを求めるには、逆関数を使います。
θ＝arccos（cosα２cosα１cosβ２cosβ１＋cosα２sinα１cosβ２sinβ１＋sinα２sinβ２）
これでなす角が求まりました。この値から球面上の経路距離を求めるには、１周360度の内の角度θぶんの比率を求めて、円周の長さを掛けてやればいいわけです。ラジアン角に注意して求める長さをｎとすると、
ｎ＝２πｒθ／２π
＝ｒθ
ま、こんなもんでしょ。ラジアン角を使ったから最後はこんな値になった、ということで妙に納得して、今回はこれにておわり。
2001/12/09 追記
sinθ＝[αβ]／｜α｜｜β｜ となっていた記述をcosθ＝[αβ]／｜α｜｜β｜ に修正。
２年以上この間違いを放置していたことにショック。
指摘して頂いた鹿児島大学の方、ありがとうございました。
mail:
←「\」は「@」に変えてください。