Koch's Curve (Python3)

Fractal: Koch's Curve (Python3)

Applied rule of recursive drawing	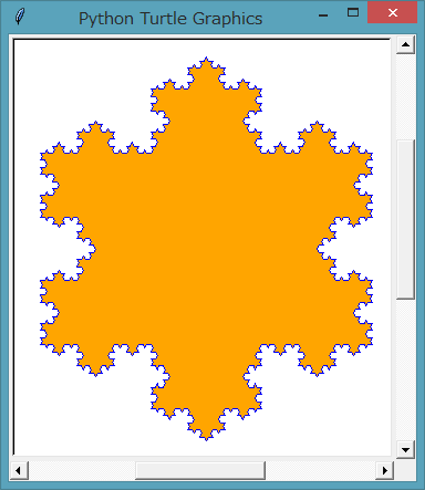This closed curve is obtained by series connection of three Koch's curves with 3-folded rotation.
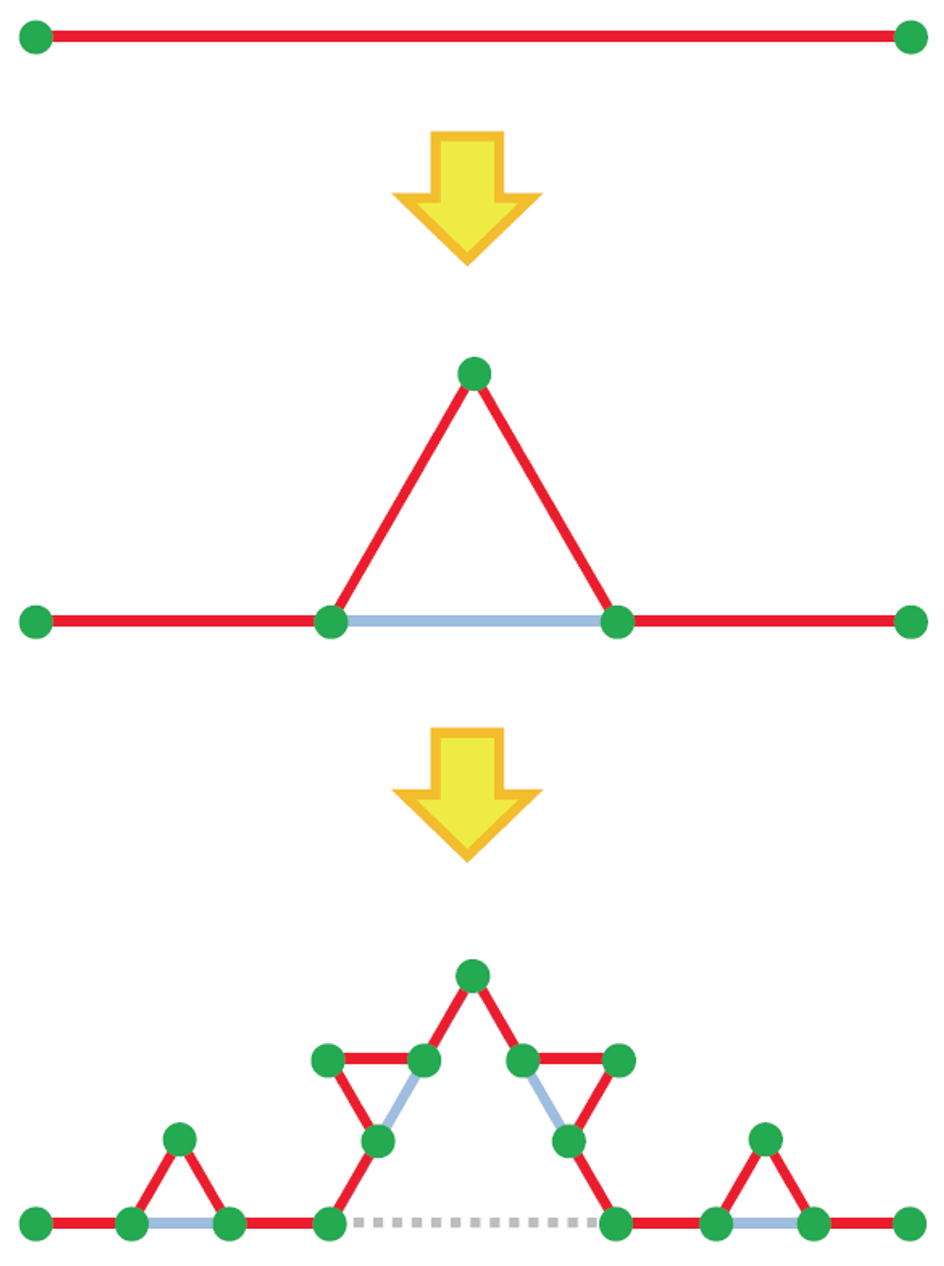
This figure indicates an applied rule of recursive drawing. When the complexity order is increased, additional green points and new red-lined paths are generated in the same manner. Here, a set of a fractional ratio of 1/3 in length and turning angles of {60^o in left, 120^o in right and 60^o in left} is always inherited for all the order.

#   KochCurve003.py
#   Combination of Three Koch's Curves
#   on Python 3.4.1, Oct. 2, 2014
#   by Masao Sakuraba
#   (Complexity <= 4; within 1 min)

from turtle import *
import time

def InitializePosition(Length):
    screensize(Length * 3, Length * 3)
    up()
    home()
    goto(- Length / 2, Length / 2)
    down()

def PatternGenerator(L, n, c):
    if n >= c:
        forward(L)
    else:
        PatternGenerator(L / 3, n + 1, c)
        left(60)
        PatternGenerator(L / 3, n + 1, c)
        right(120)
        PatternGenerator(L / 3, n + 1, c)
        left(60)
        PatternGenerator(L / 3, n + 1, c)

if __name__ == '__main__':
    start = time.clock()

    Complexity = 4
    Length = 300
    Rotation = 3

    hideturtle()
    speed(0) # “fastest”: 0, “slowest”: 1 -> “fast”: 10
    InitializePosition(Length)
    color('blue', 'orange')
    width(1)
    begin_fill()

    for i in range(Rotation):
        PatternGenerator(Length, 0, Complexity)
        right(360 / Rotation)

    end_fill()

    stop = time.clock()
    time = stop - start
    time = int(time * 1000)
    time = str(time / 1000)
    print('Processing time: ' + time + ' sec')

Reference
"24.1. turtle ― Turtle graphics"
- English Site
https://docs.python.org/3.3/library/turtle.html#module-turtle
- Japanese Site
http://docs.python.jp/3.4/library/turtle.html

< Return to Computer-Related Skills >

< Return to Home >

This home page is produced by KompoZer (free and open software).