Transmission ratio through double barriers (Python3)
Transmission
ratio (t) of a particle (e.g. electron or hole in semiconductors) through double barriers, which are separated by a
quantum well, is calculated and shown by
Python3. Of course, this is strongly related to my research on the resonant tunneling diode.
Following equations used here are a set of solution obtained by
one-dimensional Schrödinger
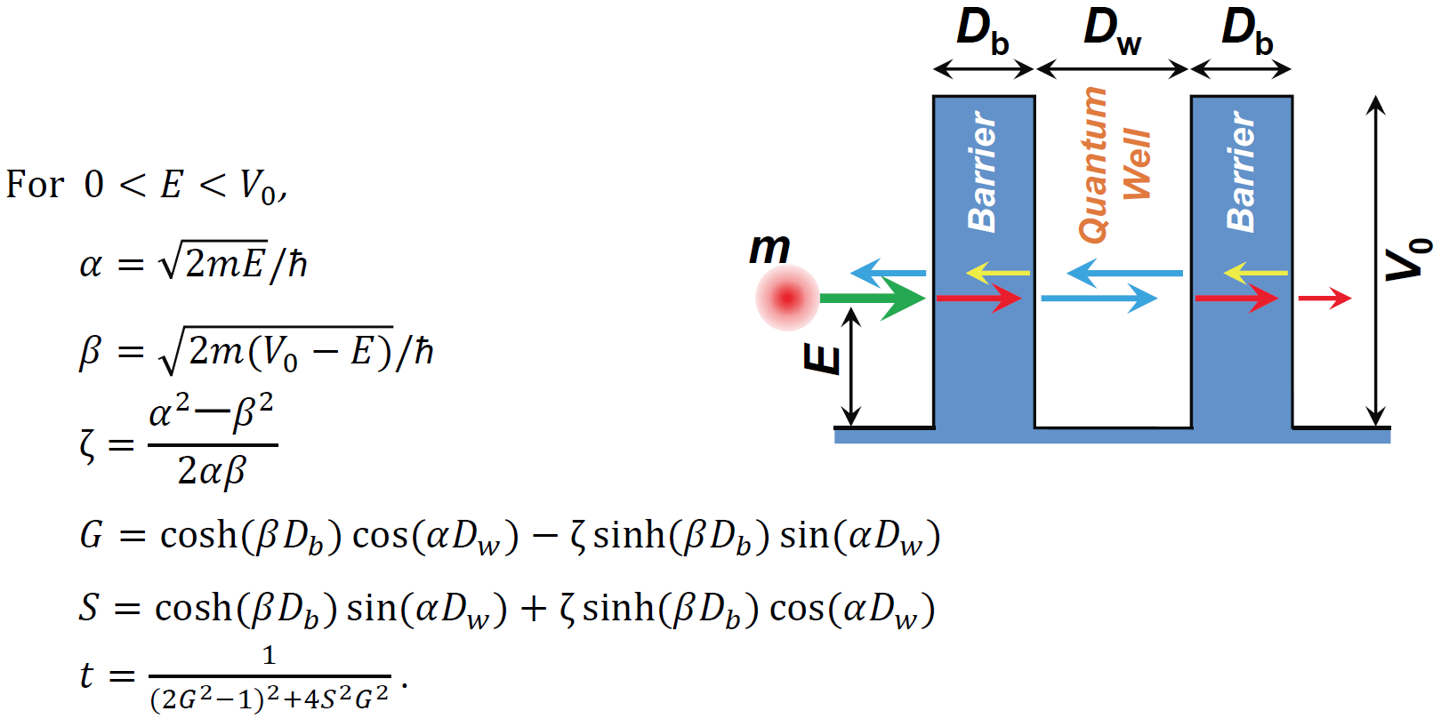
equation with typical initial condition. Height (V0) and thickness (Db) of the
barrier are 0.4 eV and 1.8 nm, respectively. Thickness of the quantum well (Dw) is 3.0 nm. Effective mass (m) of a
particle is 0.28 m0 (m0:
electron mass in vacuum).
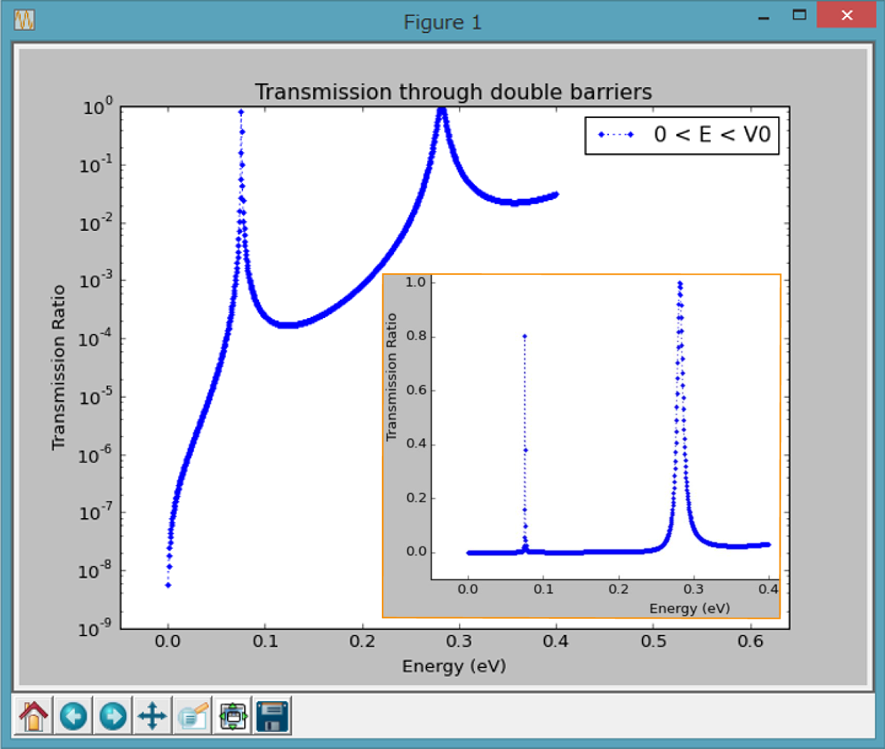
Intense quantum tunneling with resonance can be observed at specific energies (0.075 eV and 0.28 eV). Additionally, between the resonant peaks, it is clear that the transmission ratio is drastically lowered by 3-4 order of magnitude.
It
is strange that values of two peaks in resonance are close to unity
or are almost unity. Here, it should be noted that the peak value never
depends on the barrier thickness in this calculation method. When the
calculations were precisely performed with different structural
parameters, the peak value could be close to unity similarly in many cases. Does this
mean that the particle never reflects on the barrier wall and can
transmit through tha barrier without any restriction?
Here, t = 1
at two peaks was resulted by diappearance of a part of incident wave
due to interference with reflecting wave which causes one-way
transmission. It should be noted that this
does not mean diappearance of barrier ability, because incidence of
wave is surely dependent on thickness and height of barriers. Tunneling probability through single barrier
generally depends on the barrier thickness as shown by the previous calculation result.
In other
words, incidence of wave is inhibited by reflection at barriers. This suggests that an electron (or a hole) feels or knows reflection of itself before incidence!? Can you understand it?
Anyway, from these calculation results, I should conclude that the resonance makes a virtual hole in a stiff wall, and the hole surely acts as a channel for particle (wave) transmission. I believe this is one of characterstics of this universe where human beings are living now.
| #
Tunneling_double_barriers_01.py # on Python 3.4.1, Nov. 29, 2014 # by Masao Sakuraba import math import numpy import scipy import pylab def main(): meff = 0.28 # effective mass ratio of a particle V0 = 0.4 # barrier height (eV) Db = 1.8e-9 # barrier thickness (m) Dw = 3.0e-9 # quantum well thickness (m) q = 1.602e-19 # elementary charge (C) hbar = 1.0546e-34 # reduced Planck constant (J s) hbar2 = hbar ** 2 m = meff * 9.1095e-31 # absolute mass of a particle (kg) # parameters for lower energy (0 < E < V0) M = 1000 # number of energy step Alpha_d = [] Alpha_d2 = [] Beta_d = [] Beta_d2 = [] Zeta_d = [] G_d = [] S_d = [] Sinh_d = [] Sin_d = [] Cosh_d = [] Cos_d = [] t_d = [] E_d = numpy.linspace(V0 / M, V0 - V0 / M, M - 1) for i in range(M - 1): Alpha_d2.append(2 * m / hbar2 * E_d[i] * q) Alpha_d.append(math.sqrt(Alpha_d2[i])) Beta_d2.append(2 * m / hbar2 * (V0 - E_d[i]) * q) Beta_d.append(math.sqrt(Beta_d2[i])) Cosh_d.append(numpy.cosh(Beta_d[i] * Db)) Cos_d.append(math.cos((Alpha_d[i]) * Dw)) Sinh_d.append(numpy.sinh(Beta_d[i] * Db)) Sin_d.append(math.sin((Alpha_d[i]) * Dw)) Zeta_d.append( (Alpha_d2[i] - Beta_d2[i]) / (2 * Alpha_d[i] * Beta_d[i]) ) G_d.append( Cosh_d[i] * Cos_d[i] - Zeta_d[i] * Sinh_d[i] * Sin_d[i] ) S_d.append( Cosh_d[i] * Sin_d[i] + Zeta_d[i] * Sinh_d[i] * Cos_d[i] ) t_d.append( 1 / ((2 * G_d[i] ** 2 - 1) ** 2 + (4 * S_d[i] **2 * G_d[i] ** 2)) ) # 'option' : color (r,g,b,c,m,y,k,w) & line style (-,--,:,-.,.,o,^) pylab.plot(E_d, t_d, 'b:.', label='0 < E < V0') pylab.legend(loc='upper right') pylab.title('Transmission through double barriers') pylab.xlabel('Energy (eV)') pylab.ylabel('Transmission Ratio') pylab.xlim(-0.05, V0 * 1.6) pylab.yscale('log') # Delete this line, if linear y. # pylab.ylim(-0.1, 1.4) pylab.show() if __name__ == '__main__': main() |
This home page is produced by KompoZer (free and open software).