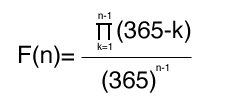
2人の場合、A君の誕生日がB君の誕生日と違う確率は、
364/365
3人の場合、A君の誕生日がB君の誕生日かつC君の誕生日と違う確率は、
364/365 x 363/365
4人の場合、A君の誕生日がB君の誕生日かつC君の誕生日かつD君の誕生日 と違う確率は、
364/365 x 363/365 x 362/365
となり、n人の誰もが誕生日が一致しない確率 F(n)は、
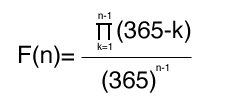
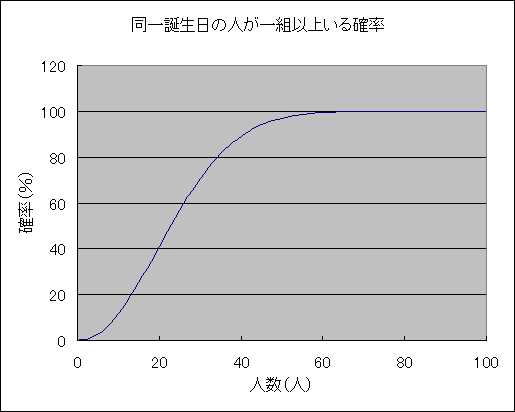
よって、求める確率 P(n)は、 P(n) = 1 - F(n) となります。これを計算すると、例えば20人の場合、41.14% , 30人の場合、70.63%になるということです。