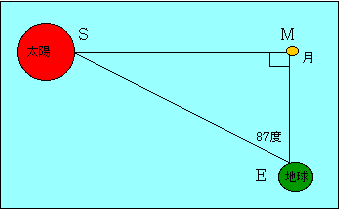
アリストテレスたちが、地球を中心にそのまわりを太陽が回っている（天動説）と考えていた頃、古代ギリシャのアリスタルコスは空に浮かぶ半月を見て次のように考えた。「月は球形だから、月のちょうど半分が照らされているのは太陽光が真横からあたっているからにちがいない。太陽Ｓ、半月Ｍ、地球Eとすれば、三角形SMEは、角ＳＭＥを直角とする直角三角形となる。ここで角SEMを測れば、角MSEも求められて直角三角形SMEの相似形がかける。そうすれば、太陽は、月の何倍の距離にあるかがわかる。月と太陽は肉眼ではほとんど同じ大きさに見えるから太陽が月の何倍の大きさか比べられる。さらに地球は月の約3倍なので太陽が地球の何倍か見当がつく。」と・・・そこでアリスタルコスは、実際に太陽と半月の角度を測定して87度を得た。角EＳＭ　90-87＝３度となる　　　　　　　　　　　　　　　　　　　　

　それで直角三角形SMEを描き、MEを基にしてSEを測ると19倍を得た。「太陽は、月の19倍大きい。地球の直径は、月の約3倍なので太陽は、地球の約6倍の大きさだ。その重さは、地球の約200倍以上となるだろう。」ここまで調べてアリスタルコスは、次のように結論づけた。
　　　　　　　　　　　　　　　　　　　　　　

　「これで太陽は、地球よりずーと大きいことがわかった。地球よりはるか に大きなものが地球のまわりを１日１回まわっていると考えるのは不自然だ。だから天動説は、まちがっている。きっと小さい地球が大きい太陽のまわりをまわっているにちがいない。」
　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　当時の測定精度は高くなかったので、かなり数字に誤差があります。実際の太陽は、距離が月までの約390倍、重さは地球の約33万倍です。しかし、これでも太陽と地球を比べる上では、まぎれもなく太陽の巨大さを推定できるものです。2000年以上前に手製の観測器具と初歩的な幾何学を用いてこれだけの結論を得たことは、すばらしいことです。これは客観的事実の上に立った数学的な帰結であり、古代人でありながらアリスタルコスの合理的な思考展開には驚かされるばかりです。（数字は、端数を略し、わかりやすい整数にしました ）
では、アリスタルコスのように実際に半月の時に角度を測ってみよう。

（2000年4月記）

次の体験記「アリスタルコスの角度を測る」へどうぞ