おせっかいおばさん元気いっぱい!!

ユニットおりがみをたのしもう

ユニットおりがみとは、部品を組み合わせて形をつくるおりがみです。

簡単な形の部品でも組み合わせることにより、幾何学的な美しい形ができあがります。

くす玉おりがみなども、部品を組み合わせて形をつくるものです。

複数の同じ形を作っておいて、最後に糊や糸で形にするものは、広い意味でのユニットおりがみといえるでしょう。

歴史

1734年に刊行された「欄間図式」という本には、6枚組の立方体に似た作品が紹介されています。

伝承のメンコや手裏剣はまさにユニットおりがみです。

1960年代、薗部光伸氏が「薗部式ユニット」を考案しました。

簡単な折り方で応用範囲がひろく、ユニットおりがみの基本といえるでしょう。

笠原邦彦氏は著書で「簡易薗部式ユニット」やたくさんの作品を紹介しました。

布施知子氏は、立体だけでなく「箱」にすることで応用分野を広げています。

美しいだけでなく、数学的な面白さから、男女を問わず、海外にもファンはたくさんいます。

たくさんたくさん

ユニットおりがみをたのしむためにはとにかくたくさんたくさんユニットをつくらなくてはなりません。

そのためにはひとつのユニットができるだけ簡単に折れたほうがいいのです。

継ぎ手の部分と継ぎ手を入れる部分さえあれば、ユニットになります。

まず折りの少ないユニットをたくさんたくさんつくってみましょう。

そのべ式ユニット

薗部光伸氏の考案したユニットは、ユニット折り紙が拡がるきっかけになった優れた折り方です。

平らな平行四辺形におれたところから、おり線をいれていきます。

おり線の数、場所、山おりと谷おりの組み合わせをしていくとさまざまな種類があります。

継ぎ手をいれる部分が2方向にありますから、変化は無限にあるのです。

そのべ式ユニットは、組み上げたときにも美しい無駄のない形をしています。

簡単でいて、6枚、12枚、30枚、…と多面体のすべてに当てはまり、折り方を少し変える応用も楽しめます。

簡易そのべ式ユニット

笠原邦彦氏の考案した薗部氏のユニットを簡単にしたものです。

多面体をつくるにはたくさんたくさんユニットを作らなくてはなりませんから、簡単なほうがいいです。

もっとも簡単なものをつかうと多面体に組み上げたときは内側にひらひら出てしまうのですが、内側は見えませんから、…。

そのべ式と簡易そのべ式の両方を混ぜて使うこともできます。

その場合は継ぎ手になる部分が右上左下なのか、右下左上なのか統一させておきましょう。

そのべ式ユニットもっと簡単に

組み上げたときに、内側で端が出たり出なかったりするのは気にしません。

とにかくたくさんたくさんのためには、簡単に、…。

おりがみのこと

市販の折り紙は15cm角が色、柄ともに豊富です。

厚さや和紙など素材の変化も楽しめます。

15cmを4等分して7.5cm角にしたものでたくさんたくさんつくりましょう。

色の組み合わせを楽しむ時には、4枚、6枚…と必要になりますから、15cm角が1枚とか1枚半とか考えるのです。

最初から7.5cm角のものを求めてもいいのですが、微妙なもので、…。

正確な正方形でないものが多いので、15cm角を4等分したほうがいいでしょう。

15cmが正確な正方形でなかったとしても、4等分すれば、誤差の範囲内になります。

ちょっと数学

幾何学といったら、敬遠したくなりますが、ピタリと法則にあてはまったものは美しさがあります。

数学的にというより、美的に気持ちのいいものです。

ユニットおりがみは正多角形、正多面体の法則にあてはまっています。

ユニットを組み上げると三角形や五角形が見えてくるのはそのためです。

対称とか、平行、相似、等しい、など、…。

平らにいうと、

線に対して両側を同じにとか、点を中心に3つとか5つ同じものをとか、…。

組み上げていくときに気をつけることは幾何学の法則にあてはめていくことなのです。

きれいな形「正多角形」

同じ長さの線をつないで形をつくるときれいです。

同じ長さの線なので、線と線をつなぐ角度はみんな同じになります。

2本の線では「直線」角度はありません。

おりがみで作るわけにはいきませんが、ピッと整ってきれいです。

形になるのは3本の線、3角形から。

同じ長さの線をつないだものは特別に「正三角形」。

安定感があって美しい。

4本の線は正四角形といわず「正方形」。

おりがみの形です。

半分に折った長四角もツルの最初の三角も身近なきれいな形です。

5本の線は「正五角形」。

ユニットおりがみを作る上でとても大事な形です。

正五角形をとなり同志にくっつけていくと球に近い立体ができあがります。

この立体を核にして組み上げていくのがユニットおりがみなのです。

6本の線の「正六角形」では立体にはなりません。

平らな面になってしまいます。絶対、五角形なのです。

6本の線の「正六角形」はハチの巣や雪の結晶にみられる均整のとれた形です。

自然界にも多くみられ、どの方向から見ても同じで、回転させたくなる形です。

線をどんどん増やしていくとだんだん円になります。

真ん丸は安心していられるきれいな形です。

プラトンの立体「正多面体」

同じ大きさの正多角形で囲まれた立体を正多面体といいます。

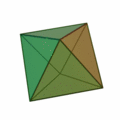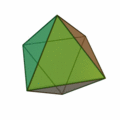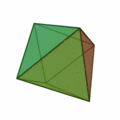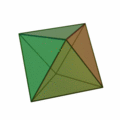
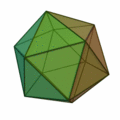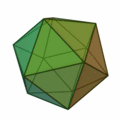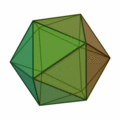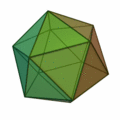
正三角形を4つ集めて正四面体。8枚集めると正八面体。20枚集めると正二十面体。

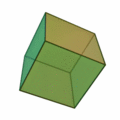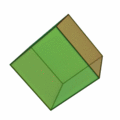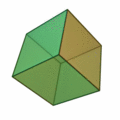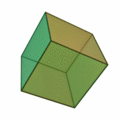
正方形を6つ集めて正六面体。普通は立方体といいます。

正五角形を12枚集めて正十二面体。

正多面体は5種類あります。

正三角形が4つで 正四面体 ↓	正三角形が8つで 正八面体 ↓	正三角形が20枚で 正二十面体 ↓
正方形が6つで 立方体(正六面体) ↓	正五角形が12枚で 正十二面体 ↓

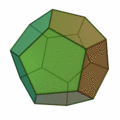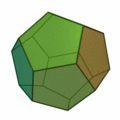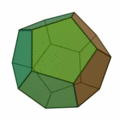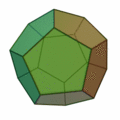ユニットおりがみは、この正多面体をたくさんのユニットで組み立てていくものです。

---

 

ご意見感想はこちらへ！

---