(1)数列
ある規則によって何番目の数は何であるか定まる数の列
(2)初項
数列をなしている各数を「項」と言い、一番最初の項を「初項」と言う
(3)一般項
一般的に数列をあらわす場合、初項を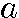 1, 第2項を
1, 第2項を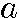 2 ,第n項を
2 ,第n項を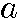 n と現す。
n と現す。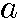 nがnについての式で書かれ、それにより数列が一般的に表されるとき、
nがnについての式で書かれ、それにより数列が一般的に表されるとき、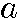 nを一般項という。
nを一般項という。
(4)等比数列
一定の数を次々掛けて得られる数列。その一定の数を公比と言う。初項を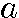 、公比をrとすると
、公比をrとすると
初項 第2項 第3項 第4項 第n項
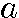
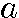 r
r 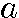 r2
r2 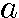 r3
r3 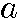 rn−1
rn−1
(定義)全ての自然数について 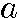 n+1 =
n+1 =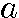 n × (公比)r
n × (公比)r
(一般項) 初項を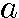 、公比をrとすると、
、公比をrとすると、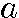 n=
n=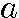 rn−1
rn−1
(5)等比数列の和
初項を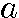 、公比をr、 末項をL、 項数がnの等比数列の和をSnとすると
、公比をr、 末項をL、 項数がnの等比数列の和をSnとすると
r≠1のとき
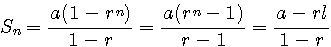
(6)無限等比級数の和
初項を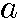 、公比をrとする無限等比数列
、公比をrとする無限等比数列  ・・・・は
・・・・は  のとき収束し、その和は
のとき収束し、その和は
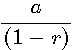 になる。
になる。
※その理由
上記(5)の式 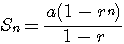 において項数nを無限大と考えると
において項数nを無限大と考えると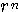 の値が
の値が だから)0になるので分子の「
だから)0になるので分子の「 」は
」は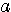 になる。
になる。