皇帝の正しくないチェス

9.2.2 キングとポーン vs キング その２

その５

図−5.1 【図−5.1】

　白のポーンがクイーンに成れるのはキングが伴って行くときに限られる。それもキングがポーンの前にいき、しかもオポジショ ンをとらなければならない。

一方黒は、その１で示した図−2.5になるように自軍のキングを正確な位置に動かさなければならない。

白の手番

1 Kf2 Kf8
2 Kf3 Kf7
3 Ke4 Ke6
4 e3! Kd6
5 Kf5 Ke7
6 Ke5!（図−5.2）
図−5.2
【図−5.2】

　１手目は1.Kd2でも良く、いずれにせよ白はけっしてポーンを進めてはいけない。
　今だと白はキングをポーンの前に配置する間があり、それゆえに勝つことができる。

　黒は1. ... Kf8として、いわゆる「デスタンス オポジション」をとっている。
　すなわちキングが互いに奇数枡離れたところで向かい合い、相手の手番にする。
　しかしこの局面での黒の場合はたいして意味がない、それは白に「手待ち」ができるポーンを持っているからである。

　3. ... Ke6と黒は引き続きオポジションをとっているが白には「手待ち」ができる。

　4. ... Kd6のところ、4. ... Kf6なら5.Kd5である。

　6.Ke5!のところ、6.e4?はできない。
　6. ... Kf7となって黒がオポジションを取り引分け。

6 ... Kd7
7 Kf6 Ke8
8 e4 Kf8
9 e5 Ke8
10 Ke6!（図−5.3）
図−5.3
【図−5.3】

　図−5.3で白の勝ちである。

　しかし10.e6?? Kf8 11.e7+ Ke8 12.Ke6でステイルメイト。

黒の手番

1 ... Ke7
2 Kf2 Kf6
3 Kf3 Kf5
4 Ke3 Ke5
5 Kd3 Kd5
6 e3 Ke5
7 e4（図−5.4）
図−5.4
【図−5.4】

　黒の２手目は、2. ... Ke6でも良い（白のキングはe7にいけないのでドローになる）。
　しかし2. ... Kd6?? 3.Kf3! Ke5 4.Ke3で白が再びオポジションをとり勝ち。

　6.e3のところ、6.e4+とすると白のキングはポーンの前に進めないのでドローである。

　図−5.4で引分けである。
　すなわち7. ... Ke6 8.Kd4 Kd6 9.e5+ Ke7 10.Ke5 Ke8! 11.Kd6 Kd8 12.e7+ Ke8でステイルメイト。

その６

図−6.1 【図−6.1】

　攻撃側ははし端(ｈ)ポーンでは勝機はほとんどない。逆に守る方はほとんどドローになる。
　もし守備側のキングがポーンの前にくることがでるなら、h7までポーンが進んだとしても、黒のキングがg8かh8にいるれば必ずステイルメイトになる。

白の手番

1 Kg7! Ke6
2 h4 Kf5
3 h5 Kg5
4 h6（図−6.2）
図−6.2
【図−6.2】

　白の初手は絶対手で、敵のキングを肝心なところから追いやる。

　図−6.2で白の勝ち。

黒の手番

1 ... Kf8!
2 Kh7 Kf7
3 h4 Kf8
4 h5 Kf7
5 h6 Kf8
6 Kh8 Kf7
7 h7 Kf8（図−6.3）
図−6.3
【図−6.3】

　図−6.1から黒の手番で始まると、白が選択できるのはステイルメイトにするか、もしくはされるかの２つである。

　2.Kh7のところ、2.h4では2. ... Kg8 3.h5 Kh8 4.h6 Kg7 5.h7+ Kh8 6.Kh6でステイルメイト。

　6.Kh8のところ、6.Kg6では6. ... Kg8となる。

　図−6.3でステイルメイト。

その７

図−7.1 【図−7.1】

プロテクトパスポーンとトライアンギュレイションまたはコーディネイト枡（スクエア）

　プロテクトパスポーンが５段目にある時はほぼ勝つことができる。
　図−7.1では白のキングが４段目に行くことからはじめる。

1 Kd3 Kd5
2 Ke3 Ke5
3 Kf3 Kd5（図−7.2）
図−7.2
【図−7.2】

　3. ... Kd5のところ、3. ... Kf5は出来ない。

　3. ... Kf5とすると、黒のキングがbポーンの四角形（クイーンのできる枡）から外れてしまうため、4.b6で白勝ち。

4 Kf4 Kd6
5 Ke4 Ke6
6 Kd4 Kd6
7 Kc4（図−7.3）
図−7.3
【図−7.3】

　ポーンでc6の地点を抑えているので、白のキングは敵陣深く侵攻できる。

7 ... Kc7
8 Kc5 Kb7（図−7.4）
図−7.4
【図−7.4】

　8.Kc5のところ、8.Kd5が早く勝てるが、Kc5の方がいろいろ学ぶことが多い。

　図−7.4の局面で、9.b6??はひどい悪手である。
　9. ... Ka6 10.Kc6でステイルメイト。

　しかし、図−7.4で黒番であれば、すぐ黒は負ける。
　すなわち図−7.4から、1. ... Ka7 2.Kc6 または1.Kc7 2.b6+ Kb7 3.Kb5となる。
　このような状態を正確にはツークツワンクの局面と呼んでいる。そこで白の手番で勝つには手待ちの手筋を使う、すなわち「トライアンギュレイション」（三角法）という重要なテクニックを使う。
　つまりは、現在の図−7.4は白番であるが、これを黒番になるように手数を調節するのである。

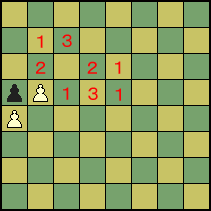
　図−7.5で数字がふってある。
　一見誤魔化し（迷わせる）のようにみえるが、考え方はいたって単純である。すでに図−7.4がツークツワンクであることがわかっている。

　白の手番：1.b6?? Ka6 　黒の手番：1. ... Ka7 2.Kc6 または1. ... Kc7 2.b6+で白勝ち。

　このことからKd6とKb6そしてKd5とKc7はツークスツワンクであることがわかる。

　Kd6（白）vs Kb6（黒）： 1. ... Kb6 2.Kd6または1. ... Kb7 2.Kc5!で、白にとってはすぐには進展はない。
　Kd5（白）vs Kc7（黒）：1. ... Kb6 Kd6または1. ... Kb7 2.Kc5で、再び白はすぐに進展はない。

図−7.5 【図−7.5】

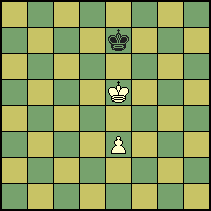
　白のキングがe5あるいはe6にある場合はどうなるか。そのときでもd5またはd6にいない限り黒のキングはb7にいたい。そこでb7に相応する枡「e5」と「e6」を「１」とナンバーをつける。
　(事実「４」という数字をこのe5/e6の枡につけるなら、厳密な意味からいえばそれに対応する黒の枡はない。数字そのものはそれ自体になにも意味をもたず、それは考えるのを助けるためにある)

　e5とe6がb7と対応するという考えを示している。白のキングが「１」の番号の枡に進みさらに次も「１」の枡に進める。すると黒はb7を離れざるを得なくなり、ここで「コーディネイト」がくずれる。しかも黒にとってさらに悪いことはc6にいけないことである。
　黒は負けである。

　では、改めて図−7.4から･･･。

1 Kd5 Kc7
2 Ke6 Kb7
3 Ke5!（図−7.6）
図−7.6
【図−7.6】

　図−7.6で黒はツークツワンクになり、コーディネイトが崩れてしまう。

3 ... Kc7
4 Kd5 Kb6
5 Kd6 Kb7
3 Kc5（図−7.7）
図−7.7
【図−7.7】

　図−7.7で白の勝ちである。

トライアンギュライション（三角法）

　もし上記のコーディネイトスクエアの考えが好きでないなら、このあとに述べることで簡単にわかる。

　白の２手目から4手目で三角形を描くように進み、このときに手待ちができる。黒のキングはこれが（手待ち）できない。
　手待ちによって白は三角形を使うと黒は2個所しか動けず白の勝ちになる。

TOP INDEX << PREV NEXT >>